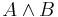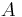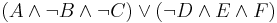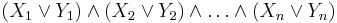Disjunctive normal form
In boolean logic, a disjunctive normal form (DNF) is a standardization (or normalization) of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more conjunctions of one or more literals. A DNF formula is in full disjunctive normal form if each of its variables appears exactly once in every clause. As in conjunctive normal form (CNF), the only propositional operators in DNF are and, or, and not. The not operator can only be used as part of a literal, which means that it can only precede a propositional variable. For example, all of the following formulas are in DNF:
However, the following formulas are NOT in DNF:
 — NOT is the outermost operator
— NOT is the outermost operator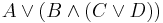 — an OR is nested within an AND
— an OR is nested within an AND
Converting a formula to DNF involves using logical equivalences, such as the double negative elimination, De Morgan's laws, and the distributive law.
All logical formulas can be converted into disjunctive normal form. However, in some cases conversion to DNF can lead to an exponential explosion of the formula. For example, in DNF, logical formulas of the following form have 2n terms:
Any particular Boolean function can be represented by one and only one full disjunctive normal form, one of the two canonical forms.
The following is a formal grammar for DNF:
- disjunct → conjunct
- disjunct → disjunct ∨ conjunct
- conjunct → literal
- conjunct → (conjunct ∧ literal)
- literal → variable
- literal → ¬variable
Where variable is thought as any variable.
See also
- Algebraic normal form
- Boolean function
- Boolean-valued function
- Conjunctive normal form
- Horn clause
- Logical graph
- Propositional logic
- Quine–McCluskey algorithm
- Truth table